(1)로지스틱 회귀분석(Logistic regression)이 가지고 있는 이야기: Binary classification, 오즈비와 로짓변환(odds ratio and logit function)

(참고: 나 문과임)

(이번글의 키워드: 오즈비, 확률, 일반회귀방정식!)

로지스틱 회귀분석이 풀고자 하는 문제 : 결과값 P를 통한 이진분류 Binary Classification

시그모이드 함수와 logistic regression 함수의 차이는 x에 어떤 값이 들어가는지 이다.

로지스틱 회귀식의 결과값은 확률 P이다. 확률의 범위는 0과 1사이에 해당한다! 그렇다면 확률을 바탕으로 풀 수 있는 문제는 어떤게 있을까? 주로 이진 분류 문제를 해결할 수 있는 것이다! (Binary Classification) 로지스틱 회귀모형의 예측 y에 대해 범위의 그래프는 좌측 그래프와 같다. 

보면 시그모이드 함수와 거의 유사해보이지 않는가? 기본적인 시그모이드 형태의 x값에 회귀방정식이 들어가기 때문에 모양도 똑같다. 일반 회귀분석에서는 예측값 yhat의 범위는 사실상 무한대 이다.

우리가 풀고 싶은 문제는 분류 문제이다. 일반회귀방정식을 통해 나온 예측값을 확률적으로 해석할 수 없다. 이를 0~1범위 로 시그모이드 함수를 통해 변환시키게 되면 확률과 같은 범위로 함수 결과가 변경되게 되면서 결과값을 확률적으로 해석 할 수 있게 된다.

 

로지스틱 회귀분석의 구성 및 해석
: 회귀계수 베타는 오즈비를 로짓변환(logit function) 한 값에 대한 영향도를 의미한다!

Y대신 p(x)라고 표기하면 더 정확해뵌다!

  앞에서 우리는 로지스틱 회귀분석이 이진분류를 해결하고자 하는 문제구나! 를 알았다. 회귀방정식이 확률의 값에 영향을 준다는 부분도 알게 되었다. 그럼 이런 질문이 떠오른다.

일반 회귀방정식에서는 회귀계수 베타 값은 x 값에 변동이 발생할 시 y 값이 얼마나 변동하는지 해석할 수 있는 단서였다!  => 그럼 로지스틱 회귀분석에서는 회귀계수 베타 값을 어떻게 해석해야할까? => 로지스틱 함수의 형태인 시그모이드 함수가 비선형 함수이기 때문에 x값 하나의 변화를 직접적으로 연결해서 해석하기 힘들다. 

이럴 때 필요한 것이 오즈비의 개념이다. 확률은 0과 1사이의 값을 가진다. 이에 상대적으로 비교하여 평가하기 용이하다는 특징이 있다! X값이 변동함에 따라 해당 사건 A가 발생할 확률이 어떻게 변하는지, 사건이 발생할 확률(P)과 그렇지 않은 확률(1-P)의 비가 얼마나 변하는지 볼 필요가 있다. 로지스틱 회귀모형에서는 회귀계수 베타의 값을 logit function에 대한 영향값으로 해석한다!!!

오즈는 통계학적으로 어떤 사건이 일어날 확률(P)을 사건이 일어나지 않을 확률(1-P)로 나눈 값을 의미한다. 이제 오즈비 공식과 로지스틱회귀모형 식을 통해 로짓변환을 유도하고, 회귀 계수 베타의 영향을 해석할 수 있는 형태로 유도해보자.

 

유도는 간단하다! 오즈비의 P 값에, 우리가 P를 구하는 방식인 로지스틱 회귀모형의 함수 값을 넣으면 된다. 이렇게 되면 오즈비는 밑은 e, 지수는 f(x)라는 아름다운 결과가 나온다!

 

 

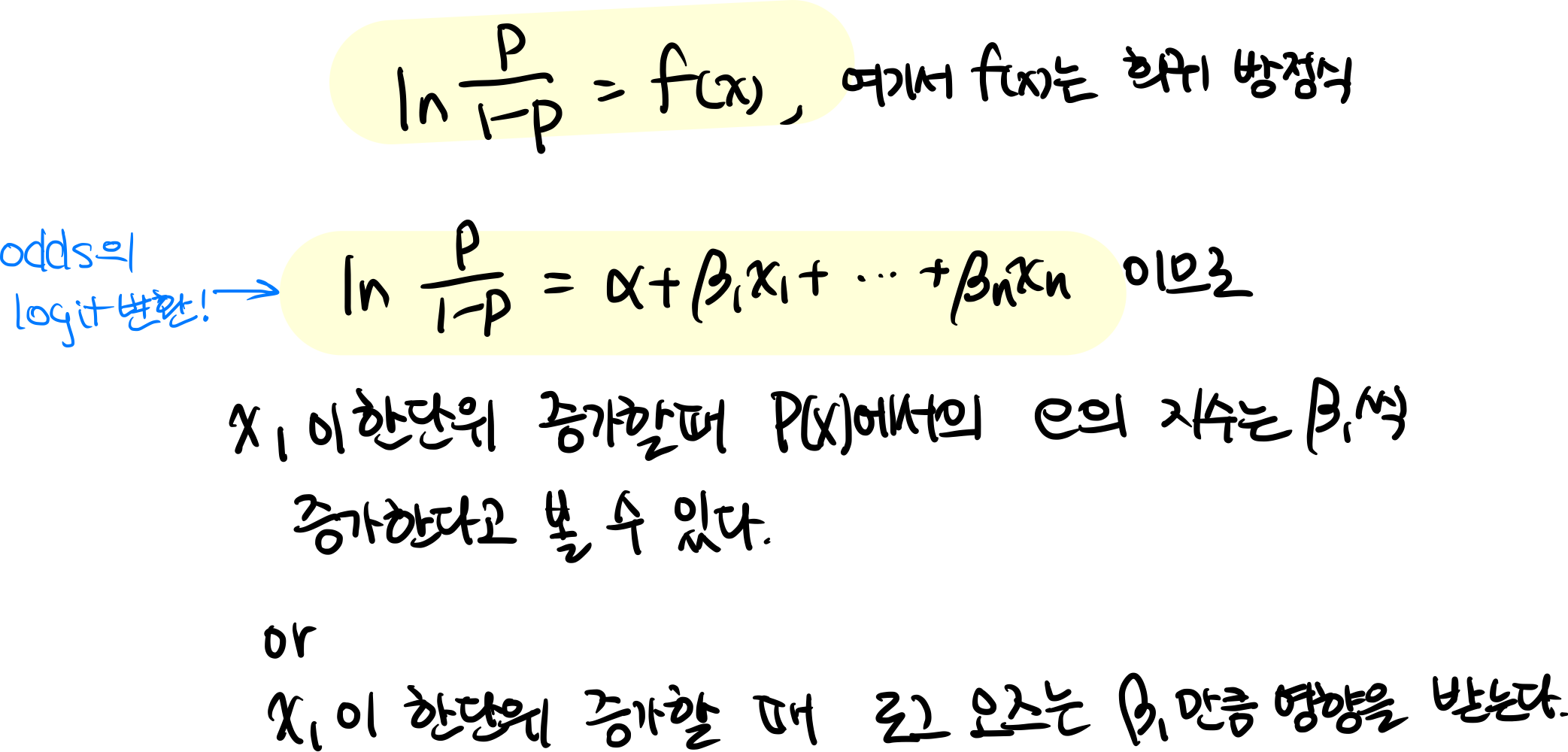
그러면 이제 회귀방정식 모양만 나오도록 양변에 밑이 자연로그를 취해보면, 회귀방정식 모양이 나오는 것을 볼 수 있다. 이 형태에서 우리는 x1이 한단위 증가할 때, beta1만큼 로그 오즈값이 증가한다는 해석을 할 수 있다. 그리고 이 로그 오즈 값은 로지스틱 회귀모형에서 e의 지수의 증감분을 의미하게 될 것이다. 

 

 

이렇게 오즈 값에 자연로그를 씌우면 로짓변환이 되는 것이다! 로짓변환(logit function)은 한마디로 오즈비를 바탕으로 로그변환을 통해 f(x)를 찾아가는 과정!이라고 할 수 있지 않을까? 더불어 비선형 함수(시그모이드)의 결과에 로그 변환을 취하여 선형성을 부여하여 해석이 가능하도록 변환하는 과정이라고 할 수 있을 것이다! 

이제 여기까지는 로지스틱 회귀모형이 확률을 어떻게 구하는지, 회귀방정식에 대한 결과를 어떻게 해석해야할지, 해석을 위해 왜 로그를 취해 로짓변환을 하는지 알아보았다!

그렇다면 또다른 질문! e의 지수 값인 f(x)는 일반 회귀방정식과 유사한 모양인데, 적절한 회귀계수 beta 값을 어떻게 찾을까?? 일반 회귀방정식처럼 OLS로 찾는걸까? 다음번에 볼 부분은 아래와 같다!

• 로지스틱이 모형을 구하는 방법: cross-validation entropy 와 maximum likelihood estimation
• (개인 적인 질문) 혹시 시그모이드 대신 하이퍼탄젠트 함수는 로지스틱 모형에 적합하지 않은가?
• 파이썬 코드 실습

 

마지막으로 오늘의 공식들을 정리해보았다!!

주절주절 글을 많이 썼지만별거 없죠?!? 역할을 알면 함수는 암기가 아니라 이해하고 자연스럽게 떠오르나봐요!!

 

 

두번째 이야기는 여기에서! 

(2)로지스틱 회귀분석(Logistic regression)이 가지고 있는 이야기: MLE(Maximum Likelihood Estimation)를 통한

 

(3)로지스틱 회귀분석(Logistic regression): 파이썬 실습(Python)